- 🏁 Aim of this Tutorial
- 🗃️ Data Preparation
- 🌱 The Default Boxplot
- 🔀 ️Sort Your Data!
- 💎 Let Your Plot Shine—Get Rid of the Default Settings
- 📊 The Choice of the Chart Type
- 💯 More Geoms, More Fun, More Info!
- 💬 Add Text Boxes to Let The Plot Speak for Itself
- 🗺️ Bonus: Add a Tile Map as Legend
- 🎄 The Final Evolved Visualization
- 💻 Complete Code for Final Plot
- 📝 Post Scriptum: Mean versus Median
🏁 Aim of this Tutorial
In this series of blog posts, I aim to show you how to turn a default ggplot into a plot that visualizes information in an appealing and easily understandable way. The goal of each blog post is to provide a step-by-step tutorial explaining how my visualization have evolved from a typical basic ggplot. All plots are going to be created with 100% {ggplot2} and 0% Inkscape.
In the first episode, I transform a basic box plot into a colorful and self-explanatory combination of a jittered dot strip plot and a lollipop plot. I am going to use data provided by the UNESCO on global student to teacher ratios that was selected as data for the #TidyTuesday challenge 19 of 2019.
🗃️ Data Preparation
I have prepared the data in the first way to map each country’s most recently reported student-teacher ratio in primary education as a tile map. I used the tile-based world data provided by Maarten Lambrechts to create this map as the first visualization for my weekly contribution:

For the second chart next to the tile map, I wanted to highlight the difference of the mean student ratio per continent but without discarding the raw data on the country-level. Therefore, I transformed the information on the region to represent the six continents excluding Antarctica (hm, do penguins not go to school?! Seems so… 🐧) and merged both data sets. If you would like to run the code yourself, you find the data preparation steps here. This is how the relevant columns of the merged and cleaned data set looks like, showing two examples per continent:
## # A tibble: 12 x 5
## indicator country region stude~1 stude~2
## <chr> <chr> <chr> <dbl> <dbl>
## 1 Primary Education Lesotho Africa 32.9 37.3
## 2 Primary Education South Africa Africa 30.3 37.3
## 3 Primary Education Bangladesh Asia 30.1 20.7
## 4 Primary Education Viet Nam Asia 19.6 20.7
## 5 Primary Education Ireland Europe 16.1 13.6
## 6 Primary Education France Europe 18.2 13.6
## 7 Primary Education Saint Vincent and the Grenadines North Ame~ 14.4 17.7
## 8 Primary Education Dominican Republic North Ame~ 18.9 17.7
## 9 Primary Education Vanuatu Oceania 26.6 24.7
## 10 Primary Education Solomon Islands Oceania 25.8 24.7
## 11 Primary Education Argentina South Ame~ NA 19.4
## 12 Primary Education Paraguay South Ame~ 24.2 19.4
## # ... with abbreviated variable names 1: student_ratio, 2: student_ratio_region🌱 The Default Boxplot
I was particularly interested to visualize the most-recent student-teacher ratio in primary education as a tile grid map per country. A usual way representing several data points per group is to use a box plot:
library(tidyverse)
ggplot(df_ratios, aes(x = region, y = student_ratio)) +
geom_boxplot()
🔀 ️Sort Your Data!
A good routine with such kind of data (qualitative and unsorted) is to arrange the box plots or any other type such as bars or violins in an in- or decreasing order to simplify readability. Since the category “continent” does not have an intrinsic order, I rearrange the box plots by their mean student-teacher ratio instead of sorting them alphabetically which is the default:
df_sorted <-
df_ratios %>%
mutate(region = fct_reorder(region, -student_ratio_region))
ggplot(df_sorted, aes(x = region, y = student_ratio)) +
geom_boxplot()
💡 Sort your data according to the best or worst, highest or lowest value to make your graph easily readable—do not sort them if the categories have an internal logical ordering, e.g. age groups or income classes!
To increase the readability we are going to flip the coordinates (note that we could also switch the variables mapped to x and y in the ggplot call but this does not work for box plots so we use and it now also works for box plots!). As some ratios are pretty close to zero, it might be also a good idea to include the 0 on the y axis. I also add some space to the right (mostly for later) which we can force by adding coord_flip()scale_y_continuous(limits = c(0, 90)) (be cautious here to use limits that are beyond the limits of your data—or better use coord_*(ylim = c(0, 90) so you’re not accidentally subsetting your data).
ggplot(df_sorted, aes(x = region, y = student_ratio)) +
geom_boxplot() +
coord_flip() +
scale_y_continuous(limits = c(0, 90))
💡 Flip the chart in case of long labels to increase readability and to avoid overlapping or rotated labels!
💡 Since the latest version 3.x.x of {ggplot2} you can also flip the orientation by switching the x and y variables:
ggplot(df_sorted, aes(x = student_ratio, y = region)) +
geom_boxplot() +
scale_x_continuous(limits = c(0, 90))The order of the categories is perfect as it is after flipping the coordinates—the lower the student-teacher ratio, the better.
💎 Let Your Plot Shine—Get Rid of the Default Settings
Let’s spice this plot up! One great thing about {ggplot2} is that it is structured in an adaptive way, allowing to add further levels to an existing ggplot object. We are going to
- use a different theme that comes with the
{ggplot2}package by callingtheme_set(theme_light())(several themes come along with the{ggplot2}package but if you need more check for example the packages{ggthemes}orhrbrthemes), - change the font and the overall font size by adding the arguments
base_sizeandbase_familytotheme_light(), - flip the axes by adding
coord_flip()(as seen before), - let the axis start at 0 and reduce the spacing to the plot margin by adding
expand = c(0.02, 0.02)as argument to thescale_y_continious(), - add some color encoding the continent by adding
color = regionto theaesargument and picking a palette from the{ggsci}package, - add meaningful labels/removing useless labels by adding
labs(x = NULL, y = "title y") - adjust the new theme (e.g. changing some font settings and removing the legend and grid) by adding
theme().
💡 You can easily adjust all sizes of the theme by calling theme_xyz(base_size = )—this is very handy if you need the same viz for a different purpose!
💡 Do not use c(0, 0) since the zero tick is in most cases too close to the axis—use something close to zero instead!
I am going to save the ggplot call and all these visual adjustments in a gg object that I name g so we can use it for the next plots.
theme_set(theme_light(base_size = 18, base_family = "Poppins"))
g <-
ggplot(df_sorted, aes(x = region, y = student_ratio, color = region)) +
coord_flip() +
scale_y_continuous(limits = c(0, 90), expand = c(0.02, 0.02)) +
scale_color_uchicago() +
labs(x = NULL, y = "Student to teacher ratio") +
theme(
legend.position = "none",
axis.title = element_text(size = 16),
axis.text.x = element_text(family = "Roboto Mono", size = 12),
panel.grid = element_blank()
)Even thought we already wrote a lot of code, the plot g is just an empty plot until with a custom theme and pretty axes but actually not a “data visualization” yet.
(Note that to include these fonts we make use of the {extrafont} package{showtext} packagesystemfonts installed. Read more about how to use custom fonts in this blog post by June Choe.)
📊 The Choice of the Chart Type
We can add any geom_ to our ggplot-preset g that fits the data, i.e. that take two positional variables of which one is allowed to be qualitative. Here are some examples that fulfill these criteria:

All of the four chart types let readers explore the range of values but with different detail and focus. The box plot and the violin plot both summarize the data, they contain a lot of information by visualizing the distribution of the data points in two different ways (see below for an explanation how to read a boxplot). By contrast, the line plot shows only the range (minimum and maximum of the data) and the strip plot the raw data with each single observation. However, a line chart is not a good choice here since it does not allow for the identification of single countries. By adding an alpha argument to geom_point(), the strip plot is able to highlight the main range of student-teacher ratios while also showing the raw data:
g + geom_point(size = 3, alpha = 0.15)
Of course, different geoms can also be combined to provide even more information in one plot:
g +
geom_boxplot(color = "gray60", outlier.alpha = 0) +
geom_point(size = 3, alpha = 0.15)
⚡ Remove the outliers of the box plot to avoid double-encoding of the same information! You can achieve this via outlier.alpha = 0, outlier.color = NA, outlier.color = "transparent", or outlier.shape = NA.
We are going to stick to points to visualize the countries explicitly instead of aggregating the data into box or violin plots.
To achieve a higher readability, we use another geom, geom_jitter() which scatters the points in a given direction (x and/or y via width and height) to prevent over-plotting:
set.seed(2019)
g + geom_jitter(size = 2, alpha = 0.25, width = 0.2)
💡 Set a seed to keep the jittering of the points fixed every time you call geom_jitter() by calling set.seed()—this becomes especially important when we later label some of the points.
💡 You can also set the seed within the geom_jitter() call by setting position = position_jitter(seed). Note that in this case the width and/or height argument needs to be placed inside the position_jitter() function as well:
g + geom_jitter(position = position_jitter(seed = 2019, width = 0.2), size = 2, alpha = 0.25)(In the next code chunks, I am going to use the redundant call of set.seed(2019) before creating the plot but do not show it each time.)
💯 More Geoms, More Fun, More Info!
As mentioned in the beginning, my intention was to visualize both, the country- and continental-level ratios, in addition to the tile map. Until now, we focused on countries only. We can indicate the continental average by adding a summary statistic via stat_summary()with a different point size as the points of geom_jitter(). Since the average is more important here, I am going to highlight it with a bigger size and zero transparency:
g +
geom_jitter(size = 2, alpha = 0.25, width = 0.2) +
stat_summary(fun = mean, geom = "point", size = 5)
Note that we could also use geom_point(aes(x = region, y = student_ratio_region), size = 5) to achieve the same since we already have a regional mean average in our data.
To relate all these points to a baseline, we add a line indicating the worldwide average:
world_avg <-
df_ratios %>%
summarize(avg = mean(student_ratio, na.rm = TRUE)) %>%
pull(avg)
g +
geom_hline(aes(yintercept = world_avg), color = "gray70", size = 0.6) +
stat_summary(fun = mean, geom = "point", size = 5) +
geom_jitter(size = 2, alpha = 0.25, width = 0.2)
💡 One could derive the worldwide average also within the geom_hline() call, but I prefer to keep both steps separated.
We can further highlight that the baseline is the worldwide average ratio rather than a ratio of 0 (or 1?) by adding a line from each continental average to the worldwide average. The result is a combination of a jitter and a lollipop plot:
g +
geom_segment(
aes(x = region, xend = region,
y = world_avg, yend = student_ratio_region),
size = 0.8
) +
geom_hline(aes(yintercept = world_avg), color = "gray70", size = 0.6) +
geom_jitter(size = 2, alpha = 0.25, width = 0.2) +
stat_summary(fun = mean, geom = "point", size = 5)
⚡ Check the order of the geoms to prevent any overlapping—here, for example, draw the line after calling geom_segment() to avoid overlapping!
💬 Add Text Boxes to Let The Plot Speak for Itself
Since I don’t want to include legends, I add some text boxes that explain the different point sizes and the baseline level via annotate(geom = "text"):
(g_text <-
g +
geom_segment(
aes(x = region, xend = region,
y = world_avg, yend = student_ratio_region),
size = 0.8
) +
geom_hline(aes(yintercept = world_avg), color = "gray70", size = 0.6) +
stat_summary(fun = mean, geom = "point", size = 5) +
geom_jitter(size = 2, alpha = 0.25, width = 0.2) +
annotate(
"text", x = 6.3, y = 35, family = "Poppins", size = 2.8, color = "gray20", lineheight = .9,
label = glue::glue("Worldwide average:\n{round(world_avg, 1)} students per teacher")
) +
annotate(
"text", x = 3.5, y = 10, family = "Poppins", size = 2.8, color = "gray20",
label = "Continental average"
) +
annotate(
"text", x = 1.7, y = 11, family = "Poppins", size = 2.8, color = "gray20",
label = "Countries per continent"
) +
annotate(
"text", x = 1.9, y = 64, family = "Poppins", size = 2.8, color = "gray20", lineheight = .9,
label = "The Central African Republic has by far\nthe most students per teacher")
)
💡 You could also create a new data set (similar to our arrows data frame below) that holds the labels and the exact position, along with some other information if needed, and add that via geom_text(data = my_labels, aes(label = my_label_column)). Note that here we also would need to create a factor for the region to match the original data!
💡 Use glue::glue() to combine strings with variables—this way, you can update your plots without copying and pasting values! (Of course, you can also use your good old friend paste0().)
… and add some arrows to match the text to the visual elements by providing start- and endpoints of the arrows when calling geom_curve(). I am going to draw all arrows with one call—but you could also draw arrow by arrow. This is not that simple as the absolute position depends on the dimension of the plot. Good guess based on the coordinates of the text boxes…
arrows <-
tibble(
x1 = c(6.2, 3.5, 1.7, 1.7, 1.9),
x2 = c(5.6, 4, 1.9, 2.9, 1.1),
y1 = c(35, 10, 11, 11, 73),
y2 = c(world_avg, 19.4, 14.16, 12, 83.4)
)
g_text +
geom_curve(
data = arrows, aes(x = x1, y = y1, xend = x2, yend = y2),
arrow = arrow(length = unit(0.07, "inch")), size = 0.4,
color = "gray20", curvature = -0.3
)
… and then adjust, adjust, adjust…
arrows <-
tibble(
x1 = c(6.1, 3.62, 1.8, 1.8, 1.8),
x2 = c(5.6, 4, 2.18, 2.76, 0.9),
y1 = c(world_avg + 6, 10.5, 9, 9, 77),
y2 = c(world_avg + 0.1, 18.4, 14.16, 12, 83.45)
)
(g_arrows <-
g_text +
geom_curve(
data = arrows, aes(x = x1, y = y1, xend = x2, yend = y2),
arrow = arrow(length = unit(0.08, "inch")), size = 0.5,
color = "gray20", curvature = -0.3
)
)
💡 Since the curvature is the same for all arrows, one can use different x and y distances and directions between the start end and points to vary their shape!
One last thing that bothers me: A student-teacher ratio of 0 does not make much sense—I definitely prefer to start at a ratio of 1!
And—oh my!—we almost forgot to mention and acknowledge the data source 😨 Let’s quickly also add a plot caption:
(g_final <-
g_arrows +
scale_y_continuous(
limits = c(1, NA), expand = c(0.02, 0.02),
breaks = c(1, seq(20, 80, by = 20))
) +
labs(caption = "Data: UNESCO Institute for Statistics") +
theme(plot.caption = element_text(size = 9, color = "gray50"))
)
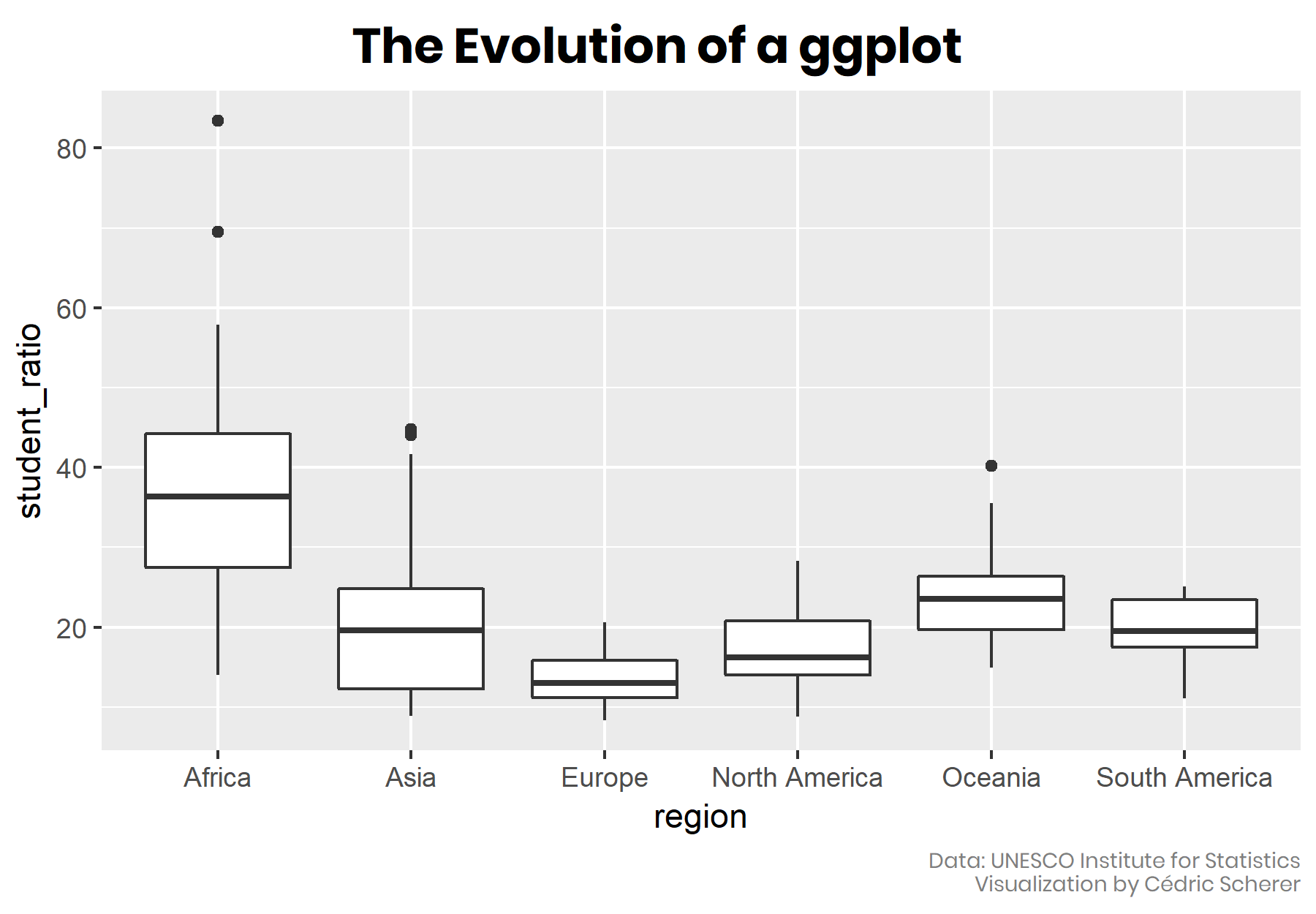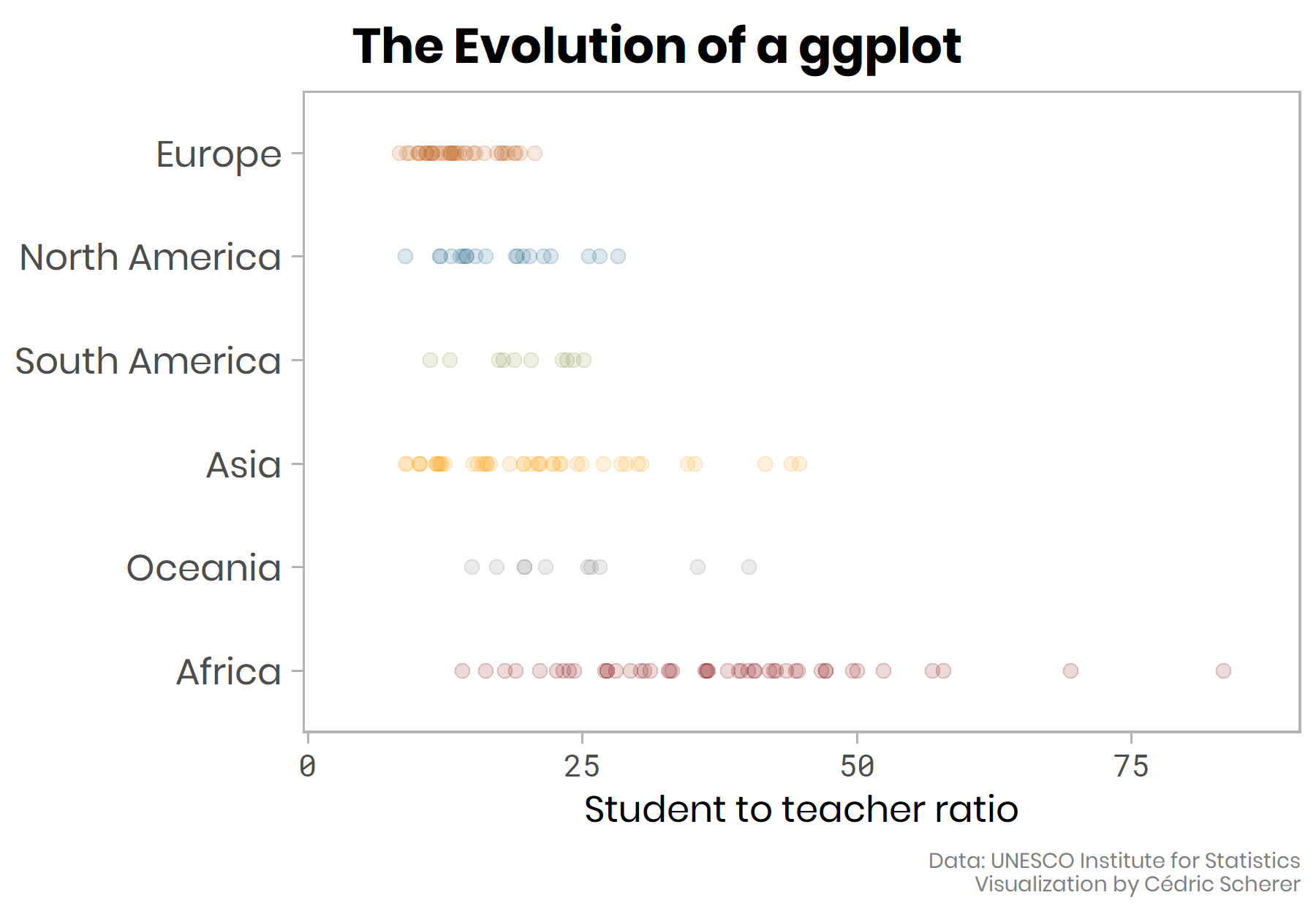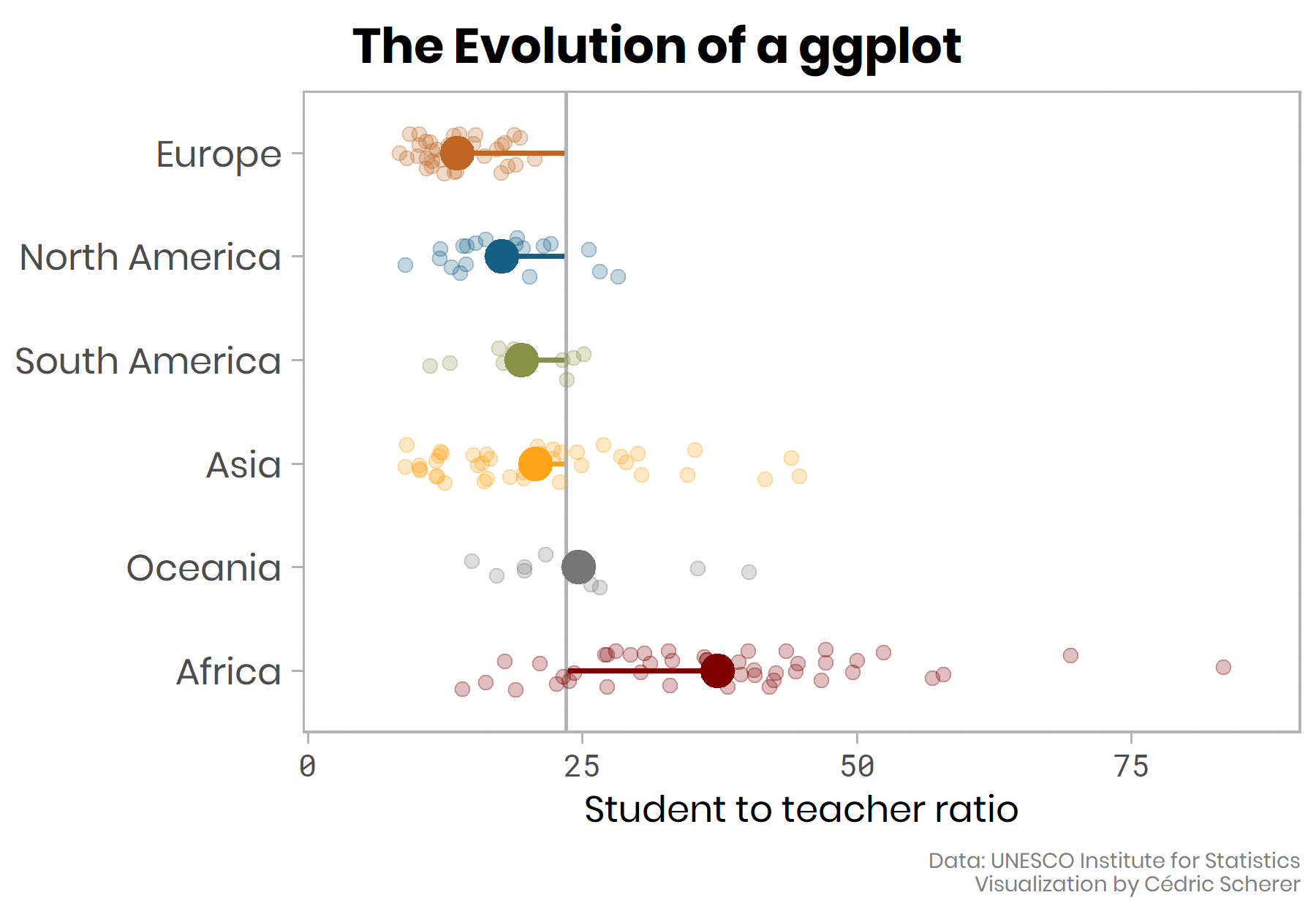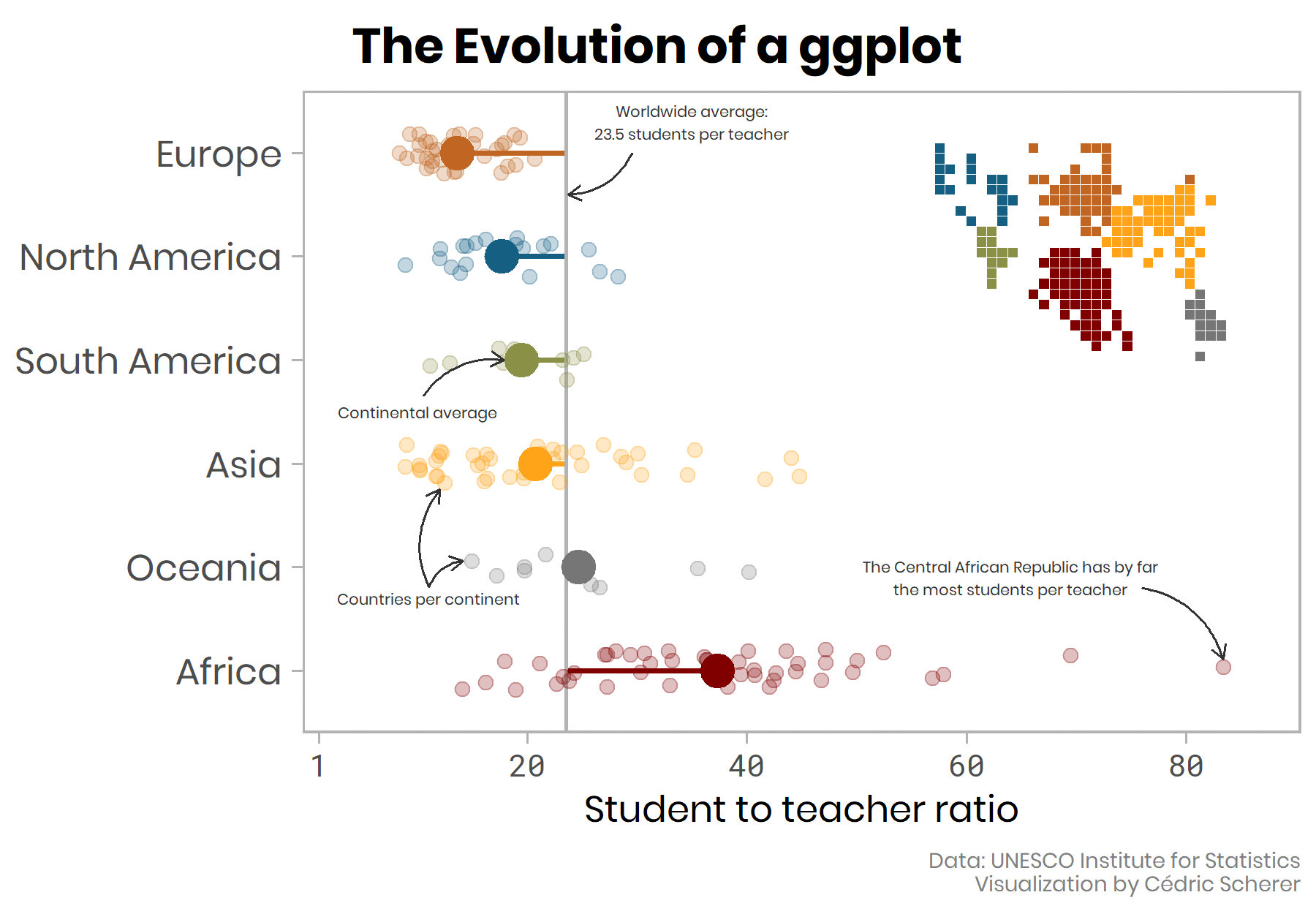
🗺️ Bonus: Add a Tile Map as Legend
To make it easier to match the countries of the second plot, the country-level tile map, to each continent we have visualized with our jitter plot, we can add a geographical “legend”. For this, I encode the region by color instead by the country-level ratios:
(map_regions <-
df_sorted %>%
ggplot(aes(x = x, y = y, fill = region, color = region)) +
geom_tile(color = "white") +
scale_y_reverse() +
ggsci::scale_fill_uchicago(guide = "none") +
coord_equal() +
theme(line = element_blank(),
panel.background = element_rect(fill = "transparent"),
plot.background = element_rect(fill = "transparent", color = "transparent"),
panel.border = element_rect(color = "transparent"),
strip.background = element_rect(color = "gray20"),
axis.text = element_blank(),
plot.margin = margin(0, 0, 0, 0)) +
labs(x = NULL, y = NULL)
)
… and add this map to the existing plot via annotation_custom(ggplotGrob()):
g_final +
annotation_custom(ggplotGrob(map_regions), xmin = 2.5, xmax = 7.5, ymin = 52, ymax = 82)
🎄 The Final Evolved Visualization
And here it is, our final plot—evolved from a dreary gray box plot to a self-explanatory, colorful visualization including the raw data and a tile map legend! 🎉

Thanks for reading, I hope you’ve enjoyed it! Here you find more visualizations I’ve contributed to the #TidyTuesday challenges including my full contribution to week 19 of 2019 we have dissected here:

💻 Complete Code for Final Plot
If you want to create the plot on your own or play around with the code, copy and paste these ~60 lines:
## packages
library(tidyverse)
library(ggsci)
library(showtext)
## load fonts
font_add_google("Poppins", "Poppins")
font_add_google("Roboto Mono", "Roboto Mono")
showtext_auto()
## get data
devtools::source_gist("https://gist.github.com/Z3tt/301bb0c7e3565111770121af2bd60c11")
## tile map as legend
map_regions <-
df_ratios %>%
mutate(region = fct_reorder(region, -student_ratio_region)) %>%
ggplot(aes(x = x, y = y, fill = region, color = region)) +
geom_tile(color = "white") +
scale_y_reverse() +
scale_fill_uchicago(guide = "none") +
coord_equal() +
theme_light() +
theme(
line = element_blank(),
panel.background = element_rect(fill = "transparent"),
plot.background = element_rect(fill = "transparent",
color = "transparent"),
panel.border = element_rect(color = "transparent"),
strip.background = element_rect(color = "gray20"),
axis.text = element_blank(),
plot.margin = margin(0, 0, 0, 0)
) +
labs(x = NULL, y = NULL)
## calculate worldwide average
world_avg <-
df_ratios %>%
summarize(avg = mean(student_ratio, na.rm = TRUE)) %>%
pull(avg)
## coordinates for arrows
arrows <-
tibble(
x1 = c(6, 3.65, 1.8, 1.8, 1.8),
x2 = c(5.6, 4, 2.18, 2.76, 0.9),
y1 = c(world_avg + 6, 10.5, 9, 9, 77),
y2 = c(world_avg + 0.1, 18.4, 14.16, 12, 83.42)
)
## final plot
## set seed to fix position of jittered points
set.seed(2019)
## final plot
df_ratios %>%
mutate(region = fct_reorder(region, -student_ratio_region)) %>%
ggplot(aes(x = region, y = student_ratio, color = region)) +
geom_segment(
aes(x = region, xend = region,
y = world_avg, yend = student_ratio_region),
size = 0.8
) +
geom_hline(aes(yintercept = world_avg), color = "gray70", size = 0.6) +
stat_summary(fun = mean, geom = "point", size = 5) +
geom_jitter(size = 2, alpha = 0.25, width = 0.2) +
coord_flip() +
annotate(
"text", x = 6.3, y = 35, family = "Poppins",
size = 2.7, color = "gray20",
label = glue::glue("Worldwide average:\n{round(world_avg, 1)} students per teacher")
) +
annotate(
"text", x = 3.5, y = 10, family = "Poppins",
size = 2.7, color = "gray20",
label = "Continental average"
) +
annotate(
"text", x = 1.7, y = 11, family = "Poppins",
size = 2.7, color = "gray20",
label = "Countries per continent"
) +
annotate(
"text", x = 1.9, y = 64, family = "Poppins",
size = 2.7, color = "gray20",
label = "The Central African Republic has by far\nthe most students per teacher"
) +
geom_curve(
data = arrows, aes(x = x1, xend = x2,
y = y1, yend = y2),
arrow = arrow(length = unit(0.08, "inch")), size = 0.5,
color = "gray20", curvature = -0.3#
) +
annotation_custom(
ggplotGrob(map_regions),
xmin = 2.5, xmax = 7.5, ymin = 52, ymax = 82
) +
scale_y_continuous(
limits = c(1, NA), expand = c(0.02, 0.02),
breaks = c(1, seq(20, 80, by = 20))
) +
scale_color_uchicago() +
labs(
x = NULL, y = "Student to teacher ratio",
caption = 'Data: UNESCO Institute for Statistics'
) +
theme_light(base_size = 18, base_family = "Poppins") +
theme(
legend.position = "none",
axis.title = element_text(size = 12),
axis.text.x = element_text(family = "Roboto Mono", size = 10),
plot.caption = element_text(size = 9, color = "gray50"),
panel.grid = element_blank()
)📝 Post Scriptum: Mean versus Median
One thing I want to highlight is that the final plot does not contain the same information as the original box plot. While I have visualized the mean values of each country and across the globe, the box of a Box-and-Whisker plot represents the 25th, 50th, 75th percentile of the data (also known as first, second and third quartile):
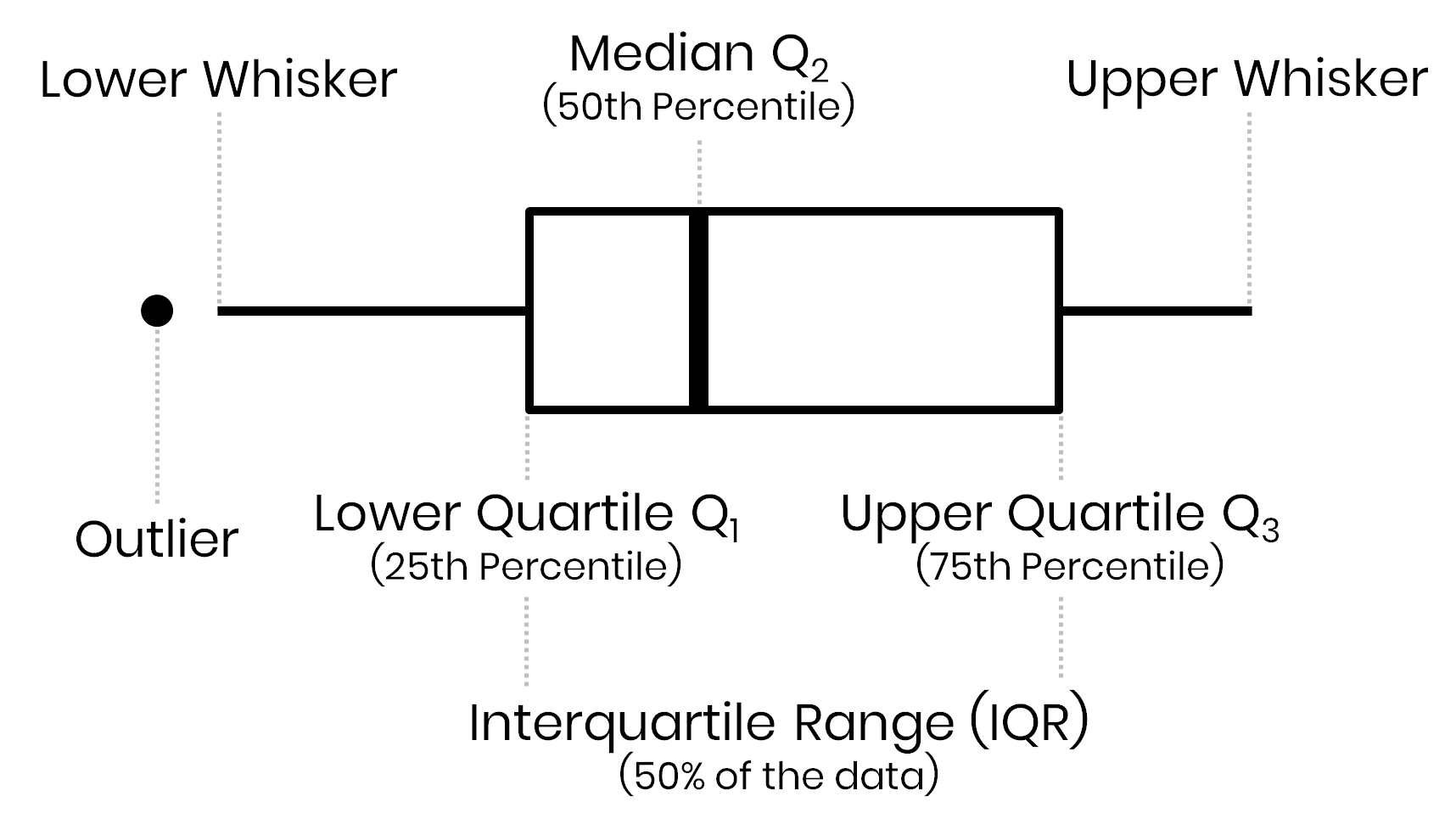
In a Box-and-Whisker plot the box visualizes the upper and lower quartiles, so the box spans the interquartile range (IQR) containing 50 percent of the data, and the median is marked by a vertical line inside the box.
The 2nd quartile is known as the median, i.e. 50% of the data points fall below this value and the other 50% are higher than this value. My decision to estimate the mean value was based on the fact that my aim was a visualization that is easily understandable to a large (non-scientific) audience that are used to mean (“average”) values but not to median estimates. However, in case of skewed data, the mean value of a data set is also biased towards higher or lower values. Let’s compare both a plot based on the mean and the median:


As one can see, the differences between continents stay roughly the same but the worldwide median is lower than the worldwide average (19.6 students per teacher versus 23.5). The plot with medians highlights that the median student-teacher ratio of Asia and Oceania are similar to the worldwide median. This plot now resembles much more the basic box plot we used in the beginning but may be harder to interpret for some compared to the one visualizing average ratios.